INCONSISTENT FORMULAS TO DETERMINE POOL VOLUME - everybody does it different, why ?

Jump to latest Follow Reply
P

PoolFLPool

Active member
Apr 25, 2022
43
USA
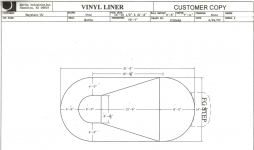
I have an oval pool 15.5x31.5 with deep end of 8.5 and shallow 3

InYoPools says take 15.5 x 31.5 x 5.75 (Avg Depth) X "6.7" which = 18,810 gallons
Doheny's says take 15.5 x 31.5 5.75 (Avg Depth) X "5.9" which is - 16564 gallons

WELL WHO THE HECK DO I LISTEN TOO ???? That is a big difference !!!!
 
Neither is correct. If your average depth is correct then you are like 17.3k. I assume its a 15x30. If the measurements inside the wall are actually 15.5x31.5 then the 18.8k measurement is correct.
 
in reality though the 16.5k is probably even closer since your transition from 3 to 8.5 likely isn't a sheer drop so half the pool isn't actually 3 and the other half 8.5
 
nwardoh said:
in reality though the 16.5k is probably even closer since your transition from 3 to 8.5 likely isn't a sheer drop so half the pool isn't actually 3 and the other half 8.5
Click to expand...
When skimmer box is 1/2 full with water, the depth of the shallow end is 3' and the depth of the deep end is 8.5' . Thoughts ? Where calculation factor should I be using ? The 5.9 or the 6.7 ?
 
PoolNJPool said:
When skimmer box is 1/2 full with water, the depth of the shallow end is 3' and the depth of the deep end is 8.5' . Thoughts ? Where calculation factor should I be using ? The 5.9 or the 6.7 ?
Click to expand...
how does it get from 3 to 8.5? Like how much of the pool is actually both depths?
 
We got you! You start with the average size to dose the chemicals. THEN adjust from the chemicals. Did you hit the mark you were aiming for? Adjust your size by 500 gallons up or down depending on what the chemical did. Mostly you will use your pH adjustment as that is the main one you will be working on. It will take some time but you will find your pools true size doing it like this.
 
  • Like
Reactions: borjis, Stump and PoolStored
nwardoh said:
how does it get from 3 to 8.5? Like how much of the pool is actually both depths?
Click to expand...
I stand corrected. Pool actual is 14'10" x 31"2" . the
nwardoh said:
how does it get from 3 to 8.5? Like how much of the pool is actually both depths?
Click to expand...
I stand corrected. Pool depth is 8 feet 5 Inches in deep end. Shallow end is 8.5 feet at a depth 3' 2" then it begins a slop down. Slope down is 13ft in legth, gradually getting deeper, before it then its 8 feet 5 inches in depth. Thanks. Again actual pool dimentions are 14'10" x 31' 2".
 

Enjoying this content?

Support TFP with a donation.

Give Support
The advice from @kimkats is best: Make a guess, dose your pool with chemicals based on that guess, then adjust your guess to match the measured results. It won't take long to zero in on the actual volume.

But if you want to calculate a good starting guess...

The flat floor at the deep end is the same size as the flat floor at the shallow end, and presumably the slope between them is symmetrical. So the pool is equivalent to one with a completely flat floor at the average depth of 69.5 inches. Length and width are 374 and 178 inches.

If your "oval" pool is actually elliptical (no straight lines, sides are curved everywhere like a squished circle), the volume is (69.5 x 374 x 178 x pi x 7.48) / (4 x 1728) = 15700 gallons. This is how the Doheny's formula works.

If the pool is actually an oval (long sides are straight, short sides are curved), the volume will be larger -- somewhere between 15700 and 20000 gallons. Easy to calculate if you post the length of the straight portion.

[edit: width is 178 inches, not 170]
 
Last edited:
DrewLG said:
The advice from @kimkats is best: Make a guess, dose your pool with chemicals based on that guess, then adjust your guess to match the measured results. It won't take long to zero in on the actual volume.

But if you want to calculate a good starting guess...

The flat floor at the deep end is the same size as the flat floor at the shallow end, and presumably the slope between them is symmetrical. So the pool is equivalent to one with a completely flat floor at the average depth of 69.5 inches. Length and width are 374 and 170 inches.

If your "oval" pool is actually elliptical (no straight lines, sides are curved everywhere like a squished circle), the volume is (69.5 x 374 x 170 x pi x 7.48) / (4 x 1728) = 15000 gallons. This is how the Doheny's formula works.

If the pool is actually an oval (long sides are straight, short sides are curved), the volume will be larger -- somewhere between 15000 and 19000 gallons. Easy to calculate if you post the length of the straight portion.
Click to expand...
Here is a diagram that may help in what you are saying. Thank you so much !!!!
 

Attachments

  • Pool Diagram0001 (2).pdf
    423 KB · Views: 5
There are no standard ovals or ellipses.

So, you have to find the area and multiply by the average depth to get cubic feet and then multiply by 7.48 to get gallons.

You have 363.1 square feet.

If the average depth is 5 feet, that gives you 1,805.5 cubic feet and 13,505 gallons.

Does the shape below match the shape of your pool?

Can you show a picture of your pool?

ellipse 89" x 187" area - Wolfram|Alpha

Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
www.wolframalpha.com www.wolframalpha.com

1657994955703.png
 
It's not really an oval or ellipse.

You can break it down into a circle and a rectangle.

The circle has a radius of 7.4375 feet, which makes π x 7.4375^2 = 173.78 square feet.

The rectangle is 16.29 feet x 14.875 feet = 242.31 square feet.

Total square feet = 416.09 feet x 5 feet = 2,080.45 cubic feet x 7.48 = 15,561 gallons, which is close to the PoolMath number.

You have to consider the deep end as less than 8 feet since the walls are sloped.

Overall, I think that 15,500 gallons is pretty close.

You can also contact Merlin with the order number and they should be able to tell you the volume.

1657996782590.png
 
Last edited:
JamesW said:
Total square feet = 416.09 feet x 5 feet = 2,080.45 cubic feet x 7.48 = 15,561 gallons.
Click to expand...

Except average depth is 69.5 inches, not 60. So 416.09 sqft x 5.79 ft = 2409.16 cubic feet x 7.48 = 18020 gallons.

JamesW said:
You can also contact Merlin with the order number and they should be able to tell you the volume.
Click to expand...

Best advice so far.
 
JamesW said:
I don't think so.

The deep end walls are sloped, so only the part in the middle is 8 feet deep.

That takes quite a bit of the volume out of the deep end.
Click to expand...
Good thing we calculated to two decimal places.

Burns' Hog Weighing Method:
  1. Find a perfectly symmetrical plank and balance it on a fulcrum.
  2. Stand the hog on one end of the plank.
  3. Pile rocks on the other end until the plank is again perfectly balanced.
  4. Guess the weight of the rocks.
 
  • Haha
Reactions: Newdude, kimkats and JamesW

Enjoying this content?

Support TFP with a donation.

Give Support
You must log in or register to reply here.
Thread Status
Hello , This thread has been inactive for over 60 days. New postings here are unlikely to be seen or responded to by other members. For better visibility, consider Starting A New Thread.
Top Bottom
Back
Jump to latest Follow Reply