Hitting Optimum Heatpump Flow

Jump to latest Follow Reply
R

russelms

Member
Aug 14, 2019
7
Syracuse, NY
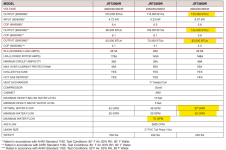
Pool Size
28000
Surface
Vinyl
Chlorine
Salt Water Generator
SWG Type
Jandy Truclear / Ei
Hi,

Our inground pool is finished being built and one question I have is in regards to hitting optimum heatpump flow.

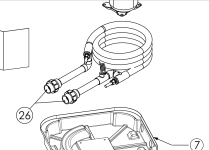
I purchased a FlowVis FV-2 and had it installed on the output of the heatpump, and just noticed while looking at this picture below that it was supposed to go between the heater and salt system not after!

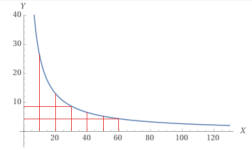
In any case the Jandy Versatemp JRT3000R says its optimum flow rate is 57gpm. I have my VS pump running at 2600RPM while heating which achieves a 60GPM measurement at the flowmeter. My interpretation is that after the salt and the headloss due to the Flowmeter the heater is nominally getting 57GPM through it and therefore achieving optimum flow and heat transfer into our pool.

Any glaring flaws in this logic?

AIL4fc9FxRwgWiZT3UQPli4SNrNRynMruaMn5JZ5ANtIYUP5jK1bjUo0VODwlXa0IvKyyMYU4cYbsm3hhfcIybFMeFl8U-ZbSDil13q-7ihWHfLgmnOlhgLnlw1XNXth3g68Gs4J5dsyeXiDJpV43JAhcAREUGiyXgwvZ5qbCtcAm2rT1310SmHTxUoLaU0oelmIcmyZKknTkOEtnKICnUHo977ylLkloXF9HK9CYHyuEHZ5AQMjOInK8_ai8Rn-jlPX2wWi7fV_Y8TVmsJya_nXPUUD2mSVEjybCSaHlte3Y0bcwly4Ij1rBrZrkdhOsHB0pg0PO4BTmpXBtHZBqWxXkx0JVYPQJabzhfihotnXZneFIHPfp9W48mJnuygilX1ECLWfDzb1x5_1wVmBqKBpQZ30O6Hqk5Jr1aULhsxQbabYGaRFww5UiovWDOkimnYVm_6SHgtbC84wlMZgVOGL8Ihvys-myNJmraaJLIclsrIfhlDWp5DH8T7Srh2i-KVOysMokiuTP8D6B2TVY4RriSxK6TFFjnlZPq4D0Hszf1XnfTMvBvnpCPUloK0CmXLvrWdX9XsSMMO1OB2JLVBdbYmws3rXLXNNP0jsFnxuNeznqyEMBg99EQo0eGzJdp-bZ8eTMl1evSzKEM1j7Iec50HcU2Gxu7mNEeX3e0x2DHVBIGEfOLdu-SB2FgWaUQ4rmIQARZ2Qx458AyNXfGEMl8bUFskS2uZz4Ggb05P_L4K-fI1-YjzOTUmDeVE7jUGScgn618xvqKEg1wZsY4uzLjnUbwCQSmrtgXDgfzVfSEJgbfke3CCfPUCP5PEbD700SXBHQ70qQNvrn56OuY77QLv3qqfwteMZyvhmbnBpTmyHUA8_wZJscicPaWy-Vw6_5jGxG08klrEiIS4C4-XfV459u54xWc7mlI3r9do6qIyWYOuzHfB-mO4F97udguZWtx4vcwvl_WtWnYnStMvsv67KqcQJIGw0WOgXDz7H9kpQfJPYH9kvSoAz92nBUiKrr0KbDGA=w2582-h1937-s-no

Thanks!
 
Unless you need more than 40 GPM, I would not go higher than 40 GPM.

If you need to go above 50 GPM, maybe consider adding a 5 lb. (PSI) check valve as a bypass.

The problem with a manual bypass is that you have to adjust it for different pump speeds.

1692726609273.png

Aquacal Bypass Valve Part #STK0135

Install a 5-lb bypass spring check valve (AquaCal P. N.: 2556, or equal to Del Industries PN: CO-0103) across the “IN” and “OUT” water ports of the heat pump.

Aqua_Cal_By_Pass_vlave.jpg


stk0135-1_500x.jpg


61L8nnKv1HL._AC_SL1000_.jpg



www.wildwestpoolsupplies.com

DEL Ozone Delcheck 5# Check Valve 2" | CO-0103

DEL Ozone CO-0103 Delcheck 5# Check Valve 2"
www.wildwestpoolsupplies.com www.wildwestpoolsupplies.com

1692726420684.png

1692726513145.png


www.poolsupplyunlimited.com

Jandy Plumbing Bypass Assembly AE-Ti | R3001900

Pool Supply Unlimited has some of the best prices when shopping for Jandy Plumbing Bypass Assembly AE-Ti | R3001900
www.poolsupplyunlimited.com www.poolsupplyunlimited.com


1692726762236.png


VersaTemp Heat Pump | Jandy

Build the perfect pool environment with Jandy professional-grade equipment. With a full line of pumps, filters, heaters, lights, valves, water sanitizers, and the automation solutions to control it all, Jandy has the complete package for any pool.
www.jandy.com www.jandy.com
 
The minimum is 30 GPM and I seriously doubt that there is any significant increase in efficiency at 57 GPM.

In my opinion, 40 GPM is plenty.

Maybe contact Jandy and ask them for engineering data that shows the difference in efficiency.

Even if there is a tiny difference, the extra power required by the pump at the higher flow rate will be more expensive than the difference in efficiency.

Pump power increases exponentially based on a cube factor.

For example, if you double the flow, it requires 23 = 8 times more power.

If the pump uses 300 watts at 30 GPM, it will require 2,400 watts at 60 GPM.

If we use $0.20 per kwH, that is $0.06 per hour at 300 watts or $0.48 per hour at 2,400 watts or $0.42 more per hour.

At "80/80/80" the heater uses 6,570 watts, which is $1.314 per hour at $0.20 per kwH.

The heat pump would need to be a lot more efficient to make the extra flow worthwhile.
 
Last edited:
Does the pump show how much power it uses?

Check the power usage at 30 GPM, 40 GPM, 50 GPM and 60 GPM.

I suspect that you can probably get plenty of flow at about 300 watts.
 
Thank you for the detailed analysis and response. The pump does not provide a power reading but I may be able to calculate it using my current clamp meter on the line that powers automation, salt, and finally pump through differential readings.

I just did a few different pump speeds and reviewed the flow-meter reading.

2600rpm = 59gpm
2100rpm = 44gpm
1950rpm = 40gpm
1750rpm = 38gpm

I've set it to 1950rpm to see how 40gpm does in regards to heating. Today's windy with some rain, the solar cover is on, and the set point is 83F with current water temp measured by the heater as 81F.

At this point I am not sure adding a pressure relief bypass is feasible - the harder thing will be explaining to my family why such a low flow-rate is acceptable. Everyone assumes faster water = hotter pool, so when they feel the returns only weekly pushing water its counter-intuitive. Any thoughts on helping explain this to others is appreciated.
 
russelms said:
Everyone assumes faster water = hotter pool, so when they feel the returns only weekly pushing water its counter-intuitive. Any thoughts on helping explain this to others is appreciated.
Click to expand...

In reality the lower the flow the hotter the output temperature is.

The faster the flow the cooler the output temperature is.

To the extent someone can feel the difference they should feel hotter water with a lower flow.

The heater puts out a fixed amount of BTU heat. Put those BTUs in less flow and the water is warmer.
 
  • Like
Reactions: JamesW
As long as the flow is above the minimum, the amount of heat added to the water is the same.

At lower flow, you are putting the heat into less water, which makes it hotter, but it transfers the same amount of heat to the pool.

At higher flow, you are putting the heat into more water, which makes it cooler, but it transfers the same amount of heat to the pool.

If you get one 5 gallon bucket of pool water at 80 degrees and one 10 gallon bucket of pool water at 80 degrees and you add 100 Btus of heat to each bucket, the water in the 5 gallon bucket will 20 degrees warmer (100 degrees) and the water in the 10 gallon bucket will get 10 degrees warmer (90 degrees).

If you pour both buckets of water back into the pool, the pool gains 100 btus from each bucket of water.

So, either way, the amount of heat added to the pool is the same.
 
Last edited:
Flow and pump speed might be irrelevant depending on what your water temp is and what temperature you are trying achieve. You need to move enough water through your heat pump to be able to absorb the max output of the heat pump. This can be figured out pretty easily, with temp readings before and after the HP, knowing the output of the HP, knowing that it takes 1 btu to heat 1 lbs of water 1 degree F and a gallon of water weighs 8.34 lbs.

To heat as quickly as possible and do it efficiently, you would water to have enough water flow through the HP so that it runs at its max and does not cycle on and off. You will likely be limited by a max flow rate through the HP. If you HP has a 100,000 btu/hr output that is (100,000/60)1666.6 btu/minute. If the max HP flowrate is 50 gpm that is (1666.6/50) 33.3 btu/gallon. This means you should see a (1666.6/8.34) 4°F temp rise from inlet to outlet. If the temp difference is less than that either the flow is to high or the HP is not putting out it's rated output (this will depend on outside air temp and how scaled the heat exchanger is). If the temp difference is higher, the flow is less than ideal (this is only going to be an issue when you get close to the max output temperature the HP is allowed to output, it may be limiting the btu output so that it does not hit one of it's safety limits).
 
  • Like
Reactions: russelms

Enjoying this content?

Support TFP with a donation.

Give Support
28,000 gallons is 233,520 pounds of water.

At 130,000 Btu per hour, that is 0.557 degrees per hour. 80˚ F Air, 80% RH, 80˚ F Water.

At 124,000 Btu per hour, that is 0.531 degrees per hour. 80˚ F Air, 63% RH, 80˚ F Water.

At 82,000 Btu per hour, that is 0.351 degrees per hour. 50˚F Air, 63% RH, 80˚F Water

Using an air temperature of about 65 degrees, I would estimate that the water should gain about 103,000 Btus per hour, which is 0.441 degrees per hour.

1692885436205.png

* Rated in accordance with AHRI Standard 1160. Test Conditions: 80˚ F Air, 80% RH, 80˚ F Water.

** Rated in accordance with AHRI Standard 1160. Test Conditions: 80˚ F Air, 63% RH, 80˚ F Water.

*** Rated in accordance with AHRI Standard 1160. Test Conditions: 50˚F Air, 63% RH, 80˚F Water
 
  • Like
Reactions: russelms
Bill1974 said:
You need to move enough water through your heat pump to be able to absorb the max output of the heat pump.
Click to expand...
The manual specifies the flow rates.

30 GPM is minimum.

57 GPM is listed as Optimal.

70 GPM is Maximum.

As long as you are within the specified flow rate, the heater should be working as it is designed.

I doubt that there is any significant difference between 30 GPM and 57 GPM.

You can ask Jandy for the difference in efficiency between 30 GPM and 57 GP.

If there a significant difference, then 30 GPM is too low and the Minimum needs to be increased.

You also need to look at the power required by the pump to pump 30 GPM vs. 57 GPM.

The pump uses about 6 times more power at 57 GPM compared to 30 GPM.

So, 250 watts at 30 GPM goes to 1,500 watts at 57 GPM.

The heat pump uses 6,570 watts, which is 6.57 kwh per hour.

If the heat transfer goes from 130,000 btu/hr (at 57 GPM) to 129,000 btu per hour (at 30 GPM), the time to heat 2 degrees goes from

130,000 btu/hr = 0.55669750 degrees per hour. 2 degrees = 3.59261538 hours.

129,000 btu/hr = 0.55241521 degrees per hour. 2 degrees = 3.62046512 hours.

The heat pump would run 0.02784974 hours (1.671 minutes, 100.259 seconds) longer.

6,820 watts (6,570 + 250) at $0.20 per kwh for 3.62046512 hours = $4.94

8,070 watts (6,570 + 1,500) at $0.20 per kwh for 3.59261538 hours = $5.80

So, as you can see, even if there was a 1,000 btu/hr difference, the cost to run the pump faster means that the total cost to gain 2 degrees is higher at higher GPM.

120,000 btu/hr = 0.51387461 degrees per hour. 2 degrees takes 3.8920 hours.

6.82 kw at $0.20 per kwh for 3.8920 hours = $5.30.

So, as you can see, even if there was a 10,000 btu/hr difference, the cost to run the pump faster means that the total cost to gain 2 degrees is higher at higher GPM.
 
  • Like
Reactions: russelms
The breakeven point is 109,892 btu/hr.

That is about 15% less efficient than 130,000 btu/hr.

0.47 degrees per hour. 2 degrees takes 4.25 hours at 6.82 kw x 0.20 = $5.80.

So, you would need to know the heat transfer to the water at different speeds as well as the pump power at different speeds to calculate which flow produces the lowest total cost when you account for the cost to run the pump and the heat pump.

In my opinion, there should not be a significant difference between 30 gpm and 57 gpm.

I would ask Jandy for their actual engineering data that supports their claim of better efficiency.

Customer Support: We're Here For You | Jandy

Email or Call Jandy at 800.822.7933. Register a product, view our warranty policy, or find a Jandy pool pro easily.
www.jandy.com www.jandy.com

[email protected]
 
I did not read the manual, but the min flow of 30 gpm may not get you the out put you are thinking. I would ask the MFG for clarity on what the heat output is at the min flow. The min flow might be so the unit does not cycle itself on and off to often and lead to an early death.

Other things to consider when heating the pool, you are also heating the ground around the pool and the lines too. There is evaporation to consider (a breeze on a dry day can suck a lot of heat out of a pool, evaporating a gallon of from the pool takes about 8700 btu's of energy, loosing a 1/4" of water in a 20' x 40' pool take about 109,000 btu's). All the number above on the water temp increase per hour are likely to the max you will see.
 
Bill1974 said:
I did not read the manual, but the min flow of 30 gpm may not get you the out put you are thinking.
Click to expand...
Can you explain what you are talking about?

How much difference is there going to be at 30, 40 50 or 60 GPM?

The water temperature does make some difference and the water will get slightly warmer at 30 GPM than 60 GPM, but I do not think that the difference is enough to offset the cost of power to run the pump at a higher speed.

If the heater was transferring 130,000 btu/hr to the water at 57 GPM, the breakeven point is 109,892 btu/hr.

That is about 15% less efficient than 130,000 btu/hr.

In other words, unless the heat transfer dropped to less than about 110,000 btu/hr, the extra power required for the pump costs more than the difference in efficiency.
 
At 30 gpm the heater may cycle on and off as its output temperature limit is reached (typically around 104°F). In this case the heater is not always putting out 130,000 Btu/hr. Once the output temperature on the heater drops a few degrees it will kick back on and continue trying to add heat to the water at 130,000 Btu/hr. It may run 4 minutes on and 1 minute off, so you are only getting 80% of the 130,000 Btu/hr output.

Pool heaters are pretty dumb, they are like driving a car but the gas peddle works like its floored (wide open) or the engine is off, there is no in between. But there are some safety features built in to keep you at speed limit. If the steepness of the hill (water flow though the heater) is big enough the car will be able to reach the speed limit (temp limit within the heater) and the car will turn off the engine (heat pump will stop moving heat from the air to the water). once the car slows down a little (temp drops) the engine will restart and run at full throttle (heat pump turn on) and the car will speed up again till it reaches the speed limit. If the road is steep enough (water flow high enough gpm) then the car will never reach the speed limit with the engine running at it's max (the pool heater will not reach the high temperature limit).

At flow less than 30 gpm the heater may be able to add so much heat to the water that the output temperature could overshoot the max output water temperature. This is bad as it could cause scalding of someone near a return jet and it could also damage the return pipe on the outlet of the pool heater. In the cars case this would be like the road is to flat and the car accelerates so quickly it would go over the speed limit once it reach the limit and the engine was shut off.
 
Bill1974 said:
At 30 gpm the heater may cycle on and off as its output temperature limit is reached (typically around 104°F).
Click to expand...
30 gpm = 1,800 gallons per hour = 15,012 pounds of water.

130,000/15,012 = 8.7 degrees temperature rise from inlet to outlet.

So, the outlet water temperature is only going to be 8.7 degrees higher than the inlet temperature.

In any case, the heater does not have a temperature sensor at the outlet, so it is not going to cycle based on outlet temperature.

If it has a high limit, the high limit is usually 135 degrees, or higher.
 
Assuming a heat transfer of 130,000 btu/hr, the equation is temp rise = 260/gpm.

At 30 gpm, the temp rise is 8.7 degrees.

At 60 gpm, the temp rise is 4.3 degrees.

If the input temp is 80 degrees and the rise is 8.7 degrees, the average temp is 84.3 degrees in the heat exchanger.

If the input temp is 80 degrees and the rise is 4.3 degrees, the average temp is 82.2 degrees in the heat exchanger.

So, you are only talking about a difference of about 2.1 degrees for the average temp in the heat exchanger.

Below is a graph of the Temp rise (Y-axis) vs. the Flow in GPM (X-axis).

Assuming an input of 80 degrees, the temp rise would need to be 24 degrees to hit 104 degrees, which happens at 10.8 GPM.

Even if the output got to 104 degrees, the heater has no way of knowing this or responding to this.

If there was a high limit, it would be at least 120 degrees, or higher.

To get a 40 degree temp rise, you would need a flow of 6.5 GPM.

At that point, the heater would begin to error out due to low flow related problems.


1693236732808.png

plot Y = 260/X, y from 2 to 40 - Wolfram|Alpha

Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
www.wolframalpha.com www.wolframalpha.com
 
Last edited:
You must log in or register to reply here.
Thread Status
Hello , This thread has been inactive for over 60 days. New postings here are unlikely to be seen or responded to by other members. For better visibility, consider Starting A New Thread.
Top Bottom
Back
Jump to latest Follow Reply